CS50AI - 第 5 章 - 神经网络
神经网络属于当下极其热门的话题,AAAI, NeurIPS 等等期刊成为了许多本科生接触科研,发表文章的首选。与神经网络相关的名词术语也往往出现在学术中,当然也出现在群聊中。
因此这节就讲一讲什么叫神经网络。
仿生学
神经网络的产生,要从人类讲起。人工智能的这一学派是链接主义,也就是通过模仿人类大脑中神经元的连接来让机器形成智能。
剩下的两大流派我们也早有接触。
一个流派是符号主义,他们主张用数理逻辑(如果…就…)来求解问题。主要在 Knowledge 这一章进行了展开。是啊,这一章中我们定义了多少符号呢!
另一个流派是行为主义,他们主张让 agent 通过与环境交互,获得奖励惩罚,从而形成更好的决策。主要在上一章 Learning 中进行了小小的展开。上一章作业中的 Nim 是一个典型的行为主义的例子。
不过,不管是什么主义,似乎,共同的理念就是让机器来解决问题,而不是人类给出一一个显式的算法。比如,计算机视觉(Computer Vision,简称 CV)中的手写数字识别,很难用一个,如果这几个像素为黑,那么就是数字几,的算法来解决问题。所以人类的处理方法是,给机器一个数据集,对输入稍加处理,让机器寻找个中的规律。
这是不是说明,人类的思考能力已经到达了上限?
或许是吧。就像以前几次工业革命一样。人怎么可能跑得过新干线呢(清濑灰二语)?君子生非异也,善假于物也。
人工智能也是一样。现在人们已经进化到了,不依靠自己的脑力解决问题,而是通过电脑自己来解决问题的阶段。感觉,硅基生命就像是一个新的物种一样。我们不清楚它是如何工作的,就像是一个黑盒子。但是,它确实能很好的解决问题。或许生物学上对牛马为何能吃苦耐劳的性格有了很深入的研究,不过,对硅基生命的研究,恐怕没那么容易。
所以,算法在人工智能领域,不再是面向问题的,而是面向 AI 的。怎样才能让 AI 更好的学习呢?
话说回来。
所以,每一个神经元都可以接收一定的输入,产生特定的输出,逐级传递。
一个最简单的例子就是或函数。有两个输入神经元,位于同一层次。它们两个连接一个输出神经元。每条边有权重,每个输出神经元自己也有一个 bias。所以一共有三个权重。根据权重和输入,可以形成一个函数。
而对于这个函数,还要进一步处理,才能实现分类的效果。
激发函数(Activation Function)
这一函数处在更高的一个层次,对原始输出进行进一步处理。大概有以下几种:
- Step Function:就是一个门槛,以 0 为界,左侧为 0,右侧(包含边界)为 1;
- Logistic Sigmoid:和上面的硬门槛相比,在边界区域形成的是缓和的曲线;
- Rectified Linear Unit(ReLU):0 左侧是 0,右侧是数值本身。即 $max(0, x)$。
进一步处理的目的是,让最终的输出落到某一类别中,从而实现分类的效果。
梯度下降算法(Gradient Descent)
我们大概已经理解了神经网络的大概结构。包含节点和边,以及一个激发函数。不过,激发函数是可以事先指定的,每条边的权重该如何获得呢?
上一章中,我们通过邻居、感知机或者其他的算法来获得了边界的位置。但,对权重,我们该如何操作呢?
解决问题的方法是「梯度下降算法」。有点数学上梯度的感觉。
这一算法的基本思路是,用随机权重初始化所有边。然后重复下列步骤:以损失(Loss) 为评判标准,对于所有输入,计算梯度向量;用梯度更新权重。
这个算法的计算是准确的,然而开销是很大的。因此,有 Stochastic Gradient Descent 算法,随机选定一个数据点。然而这一算法有点太极端了,很可能得到错误的梯度。因此, Mini-Batch Gradient Descent 算法折中,通过随机选定的几个数据点来计算梯度。
多层神经网络(Multilayer Neural Networks)
然而,不管上面的算法怎么优化,面临的问题是,它们只能对数据集进行线性的分类。
要解决这一问题,需要增加神经网络的层数,从而实现更高阶的控制。额外添加的中间层叫 Hidden Layer。
反向传播算法(Backpropagation)
多了一层,看似可以解决线性分类的问题。但是,又如何来更新每条边的权重呢?
解决问题的方案是反向传播算法。
这一算法先计算输出层的错误,然后考虑上一层中的每个单元对错误的贡献,更新权重,直到输入层为止。
这样,权重就可以被逐层更新,可以应对更深层的神经网络,即 Deep Neural Networks。
过拟合(Overfitting)
在训练的过程中,遇到的常见问题是过拟合。即,获得的权重太依赖于特定的输入(如,我们选取的训练集),而不能反映一般情况。
在上一章中,我们学习到了交叉测试的算法,这里又使用了另一种方法,叫 dropout。也就是说,每次在训练神经网络时,随机丢弃一些结点。训练多次,每次丢弃的结点不一样。这样可以保证最终获得的神经网络不依赖于特定的结点。
TensorFlow
TensorFlow 是 Google 研发的一个 Python 库,可以实现许多神经网络的相关功能。
计算机视觉(Computer Vision)
实际问题中,对图片的处理是很常见的。比如,对手写数字的识别,对水果腐烂程度的判断,对道路障碍的检测等。计算机视觉就是解决这些问题的研究领域。
图像卷积(Image Convolution)
这个词,我好久之前就接触过了。记得去年这时候,需要在英语课上进行论文的汇报。我选的是一个苹果腐烂识别的算法。
那时候对人工智能完全不懂,看到各种 Layer,无从下手。最后把 pre 糊弄完了。今天听完这次课后,对计算机视觉有关的名词,清晰多了。
为什么叫卷积呢?卷积,就是两个多项式,每项分别相乘,得到一个新的多项式。
图像的卷积,确实也是一样。为了问题的简单,这里考虑灰度图像。每个像素是 0 - 255 之间的数字。
问题 1:为什么不直接把每个像素展平,作为输入?
因为,一方面,输入的规模太大;一方面,不符合识别图像的直觉。
第一方面比较简单,这里谈谈第二方面。人类识别图像,并不是根据每个像素来识别的,而是通过一些整体特征,如弧线、边界等,来识别图片。
因此,需要综合考虑多个数据点。类似于,之前用 k-邻居 算法,现在需要通过感知机来整体考虑问题。
我们采用一个方阵作为筛子,来考虑图片的整体特征。借用官网的图片:
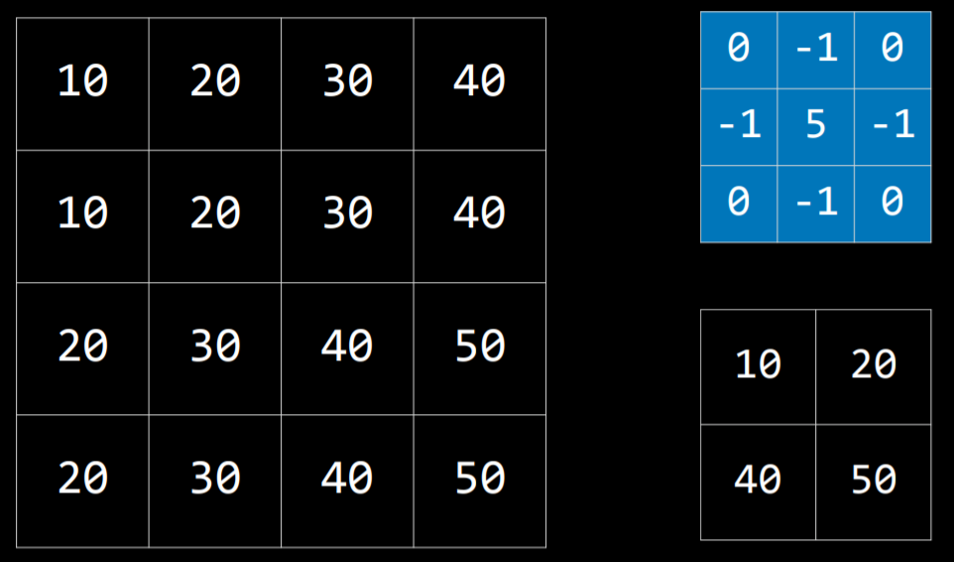
对于图片上的每个 $3 \times 3$ 区域,每个像素要和筛子上的对应位置做乘法,最后加起来,也就是卷积的定义。这样可以得到一个 $4 \times 4$ 大小的图片,包含了整体特征。
有一个方阵被常常使用:
$$
\begin{bmatrix}
-1 & -1 & -1 \
-1 & 8 & -1 \
-1 & -1 & -1
\end{bmatrix}
$$
它可以有效识别图像的边界。
池化(Pooling)
池化,也就是合并的意思。通过卷积得到的图像可能很大。这时候,通过池化就可以提取图片的共同特征。如,从 $n \times n$ 的像素集合中选择最高的,或者取平均值。
值得注意的是,图像卷积中,一个像素可能被考虑多次;而池化中,每个像素只考虑一次。
造成这一问题的原因是,图像卷积的筛选器是平移的,每次平移一个像素,直到到达边界;而池化类似于对图片进行划分,不重不漏。
在实际操作中,往往多次重复卷积和池化的步骤。
把卷积、池化和神经网络结合在一起的网络叫做 Convolutional Neural Networks。
重现神经网络(Recurrent Neural Networks)
前面讲到的神经网络都是单方向的:输入->网络->输出。
然而对于有些问题而言,网络的输出重新作为网络的输入是有帮助的,比如,用图像生成文本,视频的分类,语音识别说话人等情景。
概括一下,重现神经网络适用于多个输入(视频、音频)有依赖关系或多个输出(句子)的情景。
