CS50AI - 第 2 章 - 不确定性
不确定性(Uncertainty)
上节课讲的知识,那是布尔式的非黑即白。这里,我们考虑一个更细粒度的刻画,那就是发生的概率。
概率(Probability)
样本空间(Possible Worlds)
讨论概率,需要事先划定范围,这个范围就是样本空间。
比如,掷一个骰子,只有可能掷出来 ${1, 2, 3, 4, 5, 6}$。
概率的公理(Axioms in Probability)
有一些概率相关的道理是人们共同承认的、显而易见的:
- 所有的概率都在 $[0, 1]$ 之间;
- 样本空间中所有样本点的概率之和为 1。
无条件概率(Unconditional Probability)
考虑扔一个骰子,点数的可能;或者扔两个骰子,点数之和的可能,这种概率都是无条件的。条件的另一种理解方法就是知识。
条件概率(Conditional Probability)
条件概率,记作 $P(a | b)$,表达的含义是,在事件 $b$ 发生的情况下,$a$ 发生的概率。也可以有另外一种方式,那就是,已知 $b$ 发生了,$a$ 发生的概率。
条件概率的一个思想是缩小考虑的范围。譬如说,已经知道 $b$ 发生了,那么,那些 $b$ 未发生的情况就被我抛之脑后。现在我的目光只停留在满足条件 $b$ 的情形。
有点像剪枝,可以缩小问题的规模。
它的计算公式如下:
$$
P(a | b) = \frac{P(a \land b)}{P(b)}
$$
那么接下来是变戏法的环节。我们不考虑平凡的某个概率为 0 的情况。下面把分母移到等式另一边,就能得到这个式子:
$$
P(a \land b) = P(b)|(a | b)
$$
$$
P(a \land b) = P(a)|(b | a)
$$
它显示出一种逐层考虑的思路。不是要计算 $a, b$ 同时发生的概率吗?那我就先考虑 $a$ 发生的概率。现在我已经有了 $a$ 发生这个知识了,只需要再考虑 Given that a is true, $b$ 发生的概率。
随机变量(Random Variables)
随机变量这个概念可谓困扰了我好久。同济概率论课本是这样给出的定义:
定义 2.1 设随机试验的样本空间为 $\Omega$, 若 $X=X(\omega)$ 为定义在样本空间 $\Omega$ 上的实值单值函数, 则称 $X=X(\omega)$ 为(一维)随机变量.
用这门课的解释,那就是,随机变量是一种变量,它的取值限定在一个范围内。
比如,有一个变量 $weather$ 表示天气的情况,它的取值是 ${sunny, cloudy, rainy, windy, snowy \ldots}$。
当然,有时候我们在意定量的值。比如考虑晴天的概率、阴天的概率等等。
在中国概率论的课程中,使用列表法来清晰列出每个可能和概率;在这门课中,使用向量来表达,如 $\textbf{P}(\textit{Flight}) = <0.6, 0.3, 0.1>$,当然这就要求要实现规定顺序的对应关系。
独立性(Independence)
上面提到了这个式子:
$$
P(a \land b) = P(b)|(a | b)
$$
然而,如果 $a$ 和 $b$ 独立,又能得到什么有趣的结论呢?
首先给出独立的定义,它的含义是,知道了一件事情发生,但不影响另一件事是否发生的概率。比如,明天下雨和明天带伞,这两件事是相关的;而明天下雨和明天是星期几,这两件事就没有关系。
用数学的语言来表达,那就是:
$$
P(a | b) = P(a)
$$
这样,上面的公式就可以改写啦!
$$
P(a \land b) = P(b)P(a)
$$
当然了,两个事件很可能在直觉上有一些关系,但是,只要满足这个数值关系,我们就说,事件是独立的。
贝叶斯公式(Bayes’ Rule)
公式如下:
$$
P(b | a) = \frac{P(b) P(a | b)}{P(a)}
$$
它反映出来的一个道理是,通过一个方向的条件概率有可能求出另一方向的条件概率。比如,已知一次也不出勤的条件下考试通过的概率(先验概率),通过贝叶斯公式就能转换为已知考试通过,求次次逃课的概率(后验概率)。再比如,已知糖尿病有肥胖症状的概率,通过贝叶斯公式就能计算出,检测到患者有肥胖症状,罹患糖尿病的概率。
联合概率(Joint Probability)
联合概率是多种事件同时出现的情况,直观上,联合概率的分布是一个二维或多维表格。
比如,下雨多云,下雨不多云,不下雨多云,多云不下雨就组成了一个联合分布。
有一个规律很有趣:
$$
P(C \land rain) = P(rain) P(C | rain)
$$
这是条件概率推导出来的,这样的话,其实,我们能够得到,用 $\land$ 连接的概率分布和用 $|$ 连接的概率分布成比例,比例系数 $\alpha = P(rain)$。
概率规则(Probability Rules)
- 取反,互补($P(\lnot a) = 1 - P(a)$);
- 容斥原理($P(a \lor b ) = P(a) + P(b) - P(a \land b)$);
- 边缘化,处理联合分布的表格时常见($P(a) = P(a \land b) + P(a \land \lnot b)$);
- 条件($P(a) = P(a | b) + P(a | \lnot b)$)。
后两个可以推广到 $n$ 个变量的情形,不只是两个对立事件。
贝叶斯网络(Bayesian Networks)
贝叶斯网络表示了随机变量之间的依赖关系。
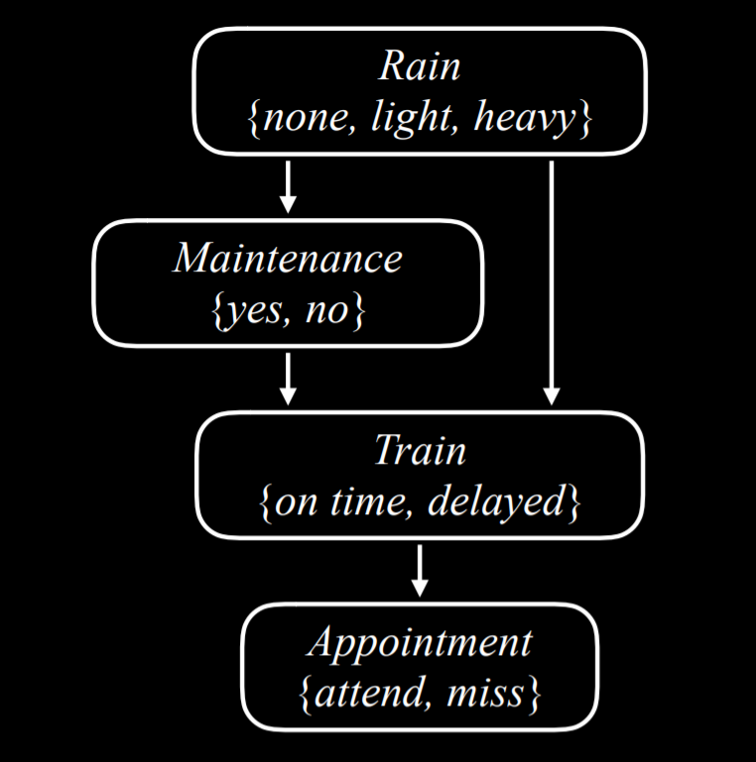
贝叶斯网络的特征是:
- 有向图
- 每个节点表示一个随机变量;
- 箭头表示因果关系;
- 每个节点存储了概率分布。
这里的因果关系,只考虑直接的关系。比如,下雨确实会影响是否能按时赴约,但并不是直接导致的。这里,赴约的直接影响因素只有火车的运行状况。
推理(Inference)
在概率论的推理中,有以下四个要素:
- 请求 X,是我们要求的随机变量;
- 证据变量 E,是已经观察到发生了某个事件的随机变量;
- 隐藏变量 Y,既不是我们要求的,也不是已经观察到发生事件的;
- 目标,计算在观察到事件的前提下,请求 X 的分布律。
举的例子是计算 $P(Appointment | (light \land no))$,这不太好求,不过我们知道,这个结果和 $P(Appointment \land light \land no)$ 成比例。
后者又如何计算呢?用边缘化,
$$
P(Appointment \land light \land no) = P(Appointment \land light \land no \land delayed) + P(Appointment \land light \land no \land \lnot delayed)
$$
之后只需要自顶向下,从没有入度的结点开始,依次进行条件概率的计算就好了。
抽样(Sampling)
有时候,这种枚举式的推断太慢,而且我们也不一定在乎特别准确的结果,大差不差就好。理论基础就是,用频率估计概率。
方法就是,从 Root 开始,依照概率逐步抽样。当然要注意,每次抽样后,掌握的知识就更多,后续的抽样也要用条件概率的方法。
最后,从中筛选出那些符合条件的样本,计算概率。
可能性权重(Likelihood Weighting)
前面的方法需要丢弃那些不符合条件的样本,比较低效。这个方法可以通过给每个样本权重来避免丢弃的问题。
思路是:
- 固定已经观察到结果的随机变量;
- 没观察到结果的随机变量,照样抽样;
- 给每个样本权重,权重指的是这个事件的所有前提条件发生的概率,也就是 $|$ 右侧的部分,不是最终的概率。
马尔科夫模型(Markov Models)
有些状态是时序相关的,从一个状态转变到另一个状态。去描述这种时间上的状态变化,使用马尔科夫模型。
马尔科夫假设(The Markov Assumption)
为了简化问题,假设一个事件只受先前某几个事件的影响,而不是无穷追溯下去。
马尔科夫链(Markov Chain)
马尔科夫链是一串随机变量的序列,其中每个随机变量都遵循马尔科夫假设。
从一个状态开始,之后基于过渡模型(transition model)就能构建出一个马尔科夫链了。
隐式马尔科夫链(Hidden Markov Chain)
有的时候,AI 只能观察到某个状态发出的信息,而无法探测到状态本身。比如 AI 能注意到有些人带了雨伞上下班,或者听到了雨滴之歌,但无法得知现在是否真的在下雨。
另一个很好的例子是,网站的运营商不知道用户是不是沉浸在提供的内容当中,但是可以通过页面的停留率或者网站的访问时间(Observation)来衡量隐式状态(Hidden State)。
传感器马尔科夫假设(Sensor Markov Assumption)
这一假设也是为了简化问题存在的。它假设证据变量,也就是我们观察到的信息,只取决于状态。比如,人们带伞只是因为下雨,而不是为了装酷或者其他原因。
通过隐式马尔科夫模型,我们可以完成:过滤(当前时间状态的分布律)、预测(未来状态的分布律)、平滑(计算过去时间的分布律)、最可能解释这些任务(基于观察,计算最可能的状态序列)。
结束
前面的贝叶斯网络有点像组合逻辑,和时间无关;后者像时序逻辑,需要有状态转移的逻辑。
