CS50AI - 第 1 章 - 知识

0. 序

这节课讲知识。在上节课的搜索中，我们的 agent 在 bfs 和 dfs 中如没头苍蝇一般，到处乱撞。然而有了启发函数和 A* 搜索后，agent 仿佛就智慧了些。

所以这节课就讲一讲，除了这种较为基础的函数来推断之外，还有哪些存储大量知识，并高效的用他们推理的技术。

1. 命题逻辑

我们最先接触到的数理逻辑概念叫命题逻辑。

1.1. 符号与连接词

命题逻辑有两个组成部分：符号和连接词。

符号很好理解，是非真即假的陈述句。几种常见的错误有疑问句、感叹句、悖论等等。

孤木不成林。连接词指的是把符号连接起来的组分，常见的有与、或、非、蕴含、等价连接词。

如果读者学习过数字逻辑和离散数学，对这些概念应该了然于胸，这里就不赘述了。补充一点，描述这些连接词的性质（什么时候真、什么时候假），经常用到的工具是真值表。

1.2. 模式

课程原文用的是 Model，如果用屈婉玲老师《离散数学》那本教材的语言，应该是赋值或解释。也就是把所有的符号都赋一个真 / 假的值。

模式的另一种解释叫 Possible World，一种可能的情形。这个词我认为很科幻、很浪漫。就像是许多平行世界一样，有的世界中，这件事发生了，而另一个世界中没有。每一个模式，就是平行世界中的一个。

1.3. 知识库

Knowledge Base 是 AI 已经知道的内容，哪些为真、哪些为假。不过可以认为存储的都是为真的陈述，因为对于假的内容，取反就成真了。

如果用《离散数学》的语言，知识库应该叫「前提」。

1.4. 蕴含

Entailment 这个词居然翻译过来是蕴含，我觉得很容易和 $\rightarrow$ 这个蕴含连接词弄混。所以采用《离散数学》的语言，应该叫「推理正确」。

它指的是，如果条件为真，结论也为真。换句话说，如果是在数学证明中，就是条件可以推出结论。

蕴含用的是这个符号 $\models$，屈婉玲老师的教材用的也是这个符号。

1.5. 推理理论

不像离散数学的教学方法，先把等值式、范式教授完毕后再进行单方向的推理的学习，这门课直接进入到了推理阶段。

似乎也可以理解，因为我们并不关心两个结论是否可以互推，只要一个可以推理出另一个就可以了。至于过程中可能出现条件减弱的情形，我们不在乎。

推理正确的定义，是在所有条件为真的情形下，结论都成立。所以直觉上，我们的想法就是，穷举那些条件为真的情形，找出这样的 Possible World，然后看，在这样的世界里，结论是否为真。

为什么不在乎那些条件为假的情形？因为根据蕴含连接词的定义，当前件为假时，公式恒为真。

这件事我一直不能理解，怎么会这样呢？经过了一学期离散数学的学习，加上这门课的再次解释，我大概清楚了。

蕴含连接词表示的是一个推断：如果…那么…

要是前件压根就不成立，这个推断并没有说明任何问题，因为推断是建立在前件为真的基础上的（如果…）。如果前件为假，我们无法从中得到任何有益内容，所以推断平凡为真。

可能还是表述的不是很清楚，就这样接受吧。

话说回来

所以如果要编写一个程序来实现的话，思路是递归式的对每个符号赋真或假。对于所有让 KB 成真的赋值，如果待验证的结论都为真，则推理正确。如果不全为真，则推理错误。

1.6. 知识工程

Knowledge engineering 是探索如何在 AI 中表示命题和逻辑的过程。如果用中文来表示的话，或许是「命题符号化」。

课程举了三个例子，一个是叫 Clue 的游戏，有点像狼人杀，不过又有一些区别。

游戏的大概流程是，分三个板块，人物、地点、武器。每个版块抽取一个放入信封，然后根据剩余的信息猜测信封中是什么。

另一个例子是一人一房，每个人有一间房，而每个房也只能装一个人。

还有一个例子是 Mastermind，有点像 Wordle，只不过这里不是单词，而是颜色。目标是把对应的颜色放到对应位置，每次排序，会返回正确位置的颜色数。

每个例子下来，符号化会越来越繁琐。

第一个例子中，如果三个板块分别有 $a$、$b$、$c$ 个对象，只需要 $a + b + c$ 个符号就完成了符号化。因为这样做已经可以确保每个符号非真即假。

第二个例子中，如果有 $n$ 个人，$n$ 个房子，就需要 $n^2$ 个符号。因为我们要确保，一个符号是非真即假的陈述句。如果仍然采用 $2 \cdot n$，每个人、每个房子作为一个符号，表明不了真假。

第三个例子则更加复杂，如果有 $m$ 种颜色，也就对应了 $m$ 个位置。需要 $m!$ 种表示。

这些都可以通过程序来实现。

1.7 推理规则

模式检查，如果进行算法分析，可以得到，这是一个指数级别的复杂度。因为如果有 $n$ 个符号，每个符号非真即假，这样就有 $2^n$ 种真值表。

还是那句话：

指数级别的复杂度不可接受！

怎样更高效的分析嘞？可以用推理规则。

这里的推理规则并不强求是等值式。不过等值式是两个方向的，单方向的推理当然成立啦。

有这样几个推理理论（不一定等值喔！）：

English	中文
Modus Ponens	假言推理规则
And Elimination	化简规则
Double Negation Elimination	双重否定律
Implication Elimination	蕴含等值式
Biconditional Elimination	等价等值式
De Morgan’s Law	德摩根律
Distributive Property	分配律

这里的推理和前一节课的搜索有隐约的联系。

一开始的初始状态是 KB，一个个推理就是 Actions，Transition Model 是变换后新的 Knowledge Base，Goal Test 是判断要证明的语句是否在知识库中，Path cost function 则记录了证明需要的步骤。

1.8. 消解证明法

这部分知识在课内没有学习过，课本上有，但老师没讲，真是很遗憾了。因为，合取范式的意义就在于可以用消解证明法来高效的证明结论是否成立啊！

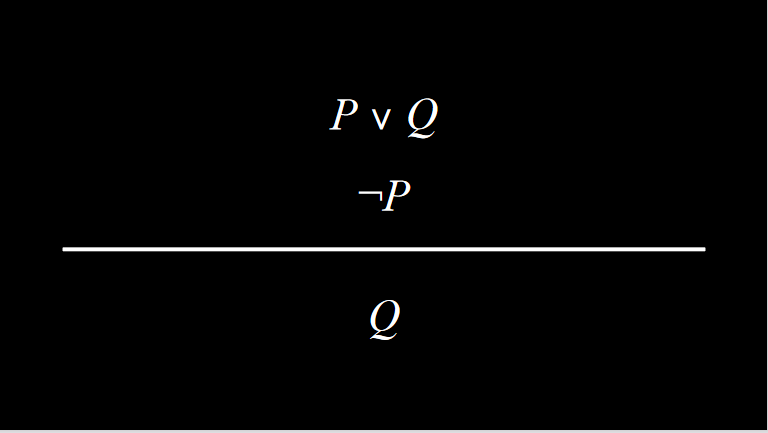
比如这个显然的例子，要么 $P$ 成立，要么 $Q$ 成立，结果 $P$ 还不成立。您猜怎么着，肯定 $Q$ 成立啊。

再看一个例子：

要么 $P$ 成立，要么 $Q$ 成立，要么 $\neg P$ 成立，要么 $R$ 成立，能推出什么呢？如果 $P$ 成立的话，$\neg P$ 不成立，这样 $R$ 必须成立；或者 $P$ 不成立，那么 $Q$ 就必须成立。哦，所以得到 $Q \lor R$

这里的 $Q$ 或者 $R$ 也可以是好多用 $\lor$ 连接起来的公式的集合。

这种形式很明显，非常高效，所以如何求得这种形式的命题公式成为了一个值得探讨的话题。这种形式的命题就是合取范式（Conjunctive Normal Form），没有主。

如何获得合取范式，不说了，太简单。来看看怎样运用消解证明法呢？

用反证法

假设结论不成立，引入到 KB 中，看看会不会推出空语句。因为空语句标志着一个命题和它的否定同时出现了。

2. 一阶逻辑

命题逻辑无法实现对事物更细粒度的刻画。

一阶逻辑包含两个符号：常量符号和谓词符号。前者表示一个对象，后者表示一种关系。

像前面那个分房的例子，我们需要 $n^2$ 个符号，而如果用一阶逻辑来表述，分别定义 $2 \cdot n$ 个人 or 房子。再定义一个谓词表示人属于这个房子。就足以表达所有的情形。这样需要的符号就显著减少了，只有 9 个，不过要表示的命题数量还是 $n^2$ 个。

在一阶逻辑中还有量词的存在，全称量词、特称量词。不再赘述了。