计组 | 校验码
这些校验码的校验原理都是:在数据位之外,增加几个校验位,用来验证传送的数据是否正确。
奇偶校验码
比较经典的奇偶校验码是在数据位之外添加一个校验位。分成两种校验方式,奇校验和偶校验。前者要求数据位和校验位中 1 的数量是奇数;后者要求 1 的数量是偶数。
检错能力:1 位;
纠错能力:0 位。
如果有两位或两位以上同时在相反方向进行了变化,则不一定检查出错误。如果说 不一定 能检查出错误,就说明纠错的能力丧失了,这种评价标准对于后续的校验方式同理。
如果有 1 位发生了错误,确实不满足校验标准,然而,到底哪一位出错呢?不知道,任何一位出错都会造成校验失败。
举个例子。
偶校验,数据是 ASCII 码的 A: 00010001,当前二进制序列已经有偶数个 1 了,校验位是 0。所以发送方发送的数据是:0 + 00010001。
如果有 1 位发生了错误,不妨是数据位的最低位,那么接收方接收到的是:0 + 0010000,不满足偶校验,检出错误。但是不知道是哪位出了错,所有的位数其中之一,都具有翻转的可能。如果有两位发生了错误,不妨设最低两位,则接收到的是 0 + 0010010,仍然满足偶校验,检查不出来。
循环冗余校验码
循环冗余校验码(CRC 码)是通过余数来检查传输错误的一种算法。它适用的场景是网络通信、光盘等可能连续出错的情况。
发送端通过把原始数据除以(这里的除是模 2 除法,可以理解为按位异或)生成多项式(生成多项式有几个要求,参见下文)得到余数,再令原始数据加上余数,目的是让修正后的数据再除以多项式余数为 0。换言之,除以生成多项式余数为 0 说明传输没有发生错误。但,如果余数不为 0,则说明发生了错误。而且,在余数的范围大于数据位长度时,可以指明哪位发生了错误。
比如,如果数据位长度为 4,生成多项式是 1011,则余数可能是 0 ~ 10,除去正常情况 0 外共有 9 种可能,足够检验每一位数据位。
接收方把数据除以生成多项式,余数为 0,编码正确。否则,余数指明了发生错误的位数。
生成多项式需要做到:
- 任何一位发生错误,余数都不能为 0(否则无法和正常情况区分了);
- 不同位发生错误,余数应该不同(否则无法检验不同位的错误了);
- 应满足余数循环规律(否则无法按补 0 的方法进行循环)。
纠错的话,因为生成多项式已经确保了余数和出错位数一一对应,所以,根据余数,通过异或出错位就可以实现纠错。不过在底层的实现上比较复杂,移位一个周期,在最高位纠正,然后再移回去。
看看笔算如何利用 CRC 码查错呢?
利用 (7, 4) 循环码,数据是:1001010,生成多项式是:1011。
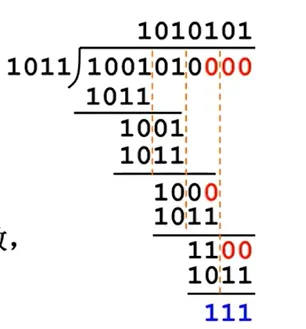
进行模二除法,也就是按位异或。商不重要,在意的是余数。把余数加上,就得到了装配后的数据。
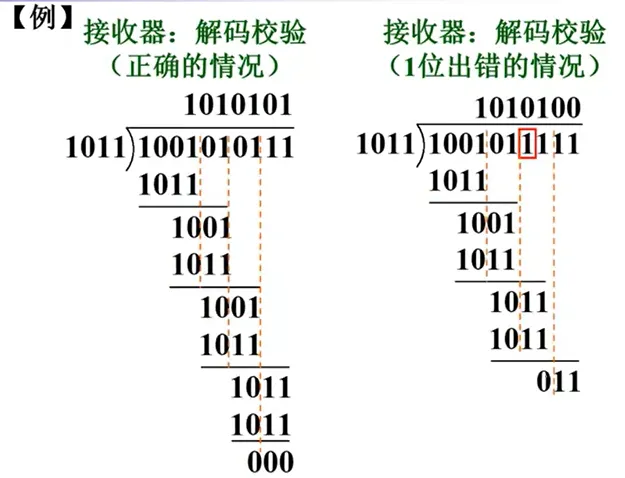
如果出现了一位错误,可以实现纠错。然而,如果发生错误的位数过多,或者校验位出了错,那就没救了。但是,CRC 码的检错能力还是比较强的。
海明码
海明码适于磁盘这种错误随机发生的系统,可以实现错误的检验和纠正。
它的核心是这个公式:
$$
2^r \geq m + r + 1
$$
其中,$r$ 表示校验位的个数;$m$ 表示数据位的个数。
对这个公式的解释如下:有 $r$ 个校验位,就有 $2^r$ 个状态,可以检测 $2^r$ 个位。
那么我们要检测多少个位呢?看等式右侧,数据位的 $m$ 个是一定要检测的;$r$ 个校验位也要检测;当然还有一个状态用来表示没有出错。
对于校验位的位置,并不像 CRC 一样在数据的末尾,而是嵌入在数据位中,在 $2^m$ 的位置。比如,$1, 2, 4, 8, 16, 32 \ldots$(从 1 开始计数)
每一个校验位的校验规则如下:
- 奇校验 or 偶校验?
- 对于每个校验位,从这位开始,检测 $m$ 位,跳过 $m$ 位…
其中,$m$ 表示校验位的位置,从 1 开始计数。如,如果一个校验位在第 4 个位置,那么它要检测的位数是 $4, 5, 6, 7, 12, 13, 14, 15\ldots$
检测到最高位为止,比如,如果一共就 12 位,后面的 $13, 14, 15$ 就不检测了。
它的取值仍然按照奇校验或者偶校验的规则,如果是偶校验,检测的数据位有奇数个 1,则取值为 1,否则为 0。
规则 2 在数学上是这样理解的,就是对于一个位置的标号,把它用 2 的幂次来表示,如果这个标号的幂次包含了校验位的位置标号,则校验位要检测它。比如,$7 = 1 + 2 + 4$,那么在 4 号的校验位就要检测它。但 $9 = 8 + 1$,那么 4 号的就不检测它。常用的技巧就是上面提到的,检测多少个,然后跳过多少个。
海明码的纠错能力是 $\lfloor \frac{n - 1}{2} \rfloor$,检错能力是 $n-1$, $n$ 是两个正确数据之间的最小汉明距离(不同位的个数)。可以想象,如果位数的变化个数没有偏离两个数中间的那条界限,是可以纠正回原来的数据的。
但是要是变化的太多,那就不知道原来的样貌了。不过,只要不变化的太多(比如,没有通过翻转 $n$ 位而导致变成了另一个合法编码),就能够检测出错误,然而这时候纠正是不可信的。
以常见的 8 位数据,4 位校验的海明码为例。因为最小海明距离为 3(每个数据位至少被 2 个校验位检测,如果一个数据位变化了,这两个校验位也会变化,形成一个新的海明码。校验位要是出错了,不在乎,因为出错后的编码非法),所以能检测 2 位错误,纠正 1 位错误。
检错的话,直接分别对校验位偶校验即可。
纠错的话,校验位出错,记为 1;否则为 0。校验位从高到低组成的二进制数表明了出错位置(仍然是从下标为 1 开始)。
