计组 | 数字在计算机中的编码
课程链接
数的表示
整数的表示
对无符号数,没必要讨论,直接按照每位的权重加起来就好了。
如何高效表示有符号数,是一个漫长的旅程。
先阐明一下设计的思路,然后再具体讲解编码的规则。
直觉上讲,如果要表示整数,如何来标记符号位呢?不妨单独开辟一个位置,来表示符号,比如 1 表示负数,0 表示正数,低位表示绝对值。这就是原码的道理所在。
不过原码有一个问题,在于 0 的表达有二义性,低位为全 0,符号位不论是 1 还是 0,都表示 0。再一个,原码的编码会让有符号数的加法运算无法利用既有的无符号数的加法电路,还要单独设计一套新的电路,不好。
因此,想要设计一个新的编码体系,让有符号数也能利用无符号数的运算电路。这样,反码诞生了。
它的规则是,正数编码不变,负数的编码是它的绝对值的编码按位取反。这样,最高位仍然是符号位,1 负 0 正。而且确实可以实现用无符号数的加法器来进行加法运算。我列了一个 3 位数的表格,读者可以加加看:
| 反码 | 真值 |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | -3 |
| 101 | -2 |
| 110 | -1 |
| 111 | -0 |
比如,$1 - 2 = 1 + (-2) = (001)_2 + (101)_2 = (110)_2 = -1$。
但还有一个问题没有解决,就是 0 还是有二义性。我推测,或许在电路上需要额外增加一些条件判断,电路会比较复杂。因此,补码诞生了。
补码不仅可以利用原先的无符号加法器,还可以消除 0 的二义性,并因此成为了目前绝大多数机器中有符号数的表示形式。补码的编码规则是,正数编码不变,负数的编码是它的绝对值的编码按位取反,然后+1。这样,最高位还是符号位,1 负 0 正。
小数的表示
整数的表示可以告一段落了,然而,小数如何来表示呢?
一开始是所谓的定点数,小数点的位置是固定的、约定好的。常见的规则是,最高位是符号位,剩下的作为数值位。小数点在符号位和数值位之间。这样,表示的是纯小数,没有整数部分。纯小数也有许多表示方法,常见的是原码的表示和补码的表示。规则和整数的一样,只不过位权可能变成了 0,-1,-2…,不再是原来的0,1,2,3…
后面,人们要表示一些更大范围、更高精度的数据,例如太阳的质量或电子的质量,定点数就不好表示了。所以让小数点浮动起来,这就是浮点型。
浮点型的编码,和科学计数法类似。比如 $9.1 \times 10^{-31}$,这里包含了几个成分:符号(+)、尾数(9.1)、指数(-31)。因此,浮点数的编码就要储存着三部分数据。
不过,为了比较数值大小的方便(一般是从高位到低位比较,而且显然比较的顺序应该是符号位、阶码、尾数),如果按照科学计数法的表达方式,有些拧巴,所以真正的浮点数在机内的表示是符号位、指数位(阶码)、尾数:

还是为了「比较」方便,所以阶码采用移码编码。移码,想要达成的一个效果就是可以让真值和编码之间达成一个线性的效果,真值大,编码值就大,反之亦然。所以补码的编码就是,选定一个偏移量,然后把真值 + 偏移量的值作为编码。比如,要表示 -4 ~ 3,那就用 000 表示 -4,然后依次递增。
偏移量的选择,是个问题。假如有 3 位的阶码,是表示 -3 ~ 4,还是 -4 ~ 3?尾数也可以有很多种表示方法,比如补码、原码等等。
标准太多啦!没有一个统一的标准,各个机器之间的兼容性就会很差。因此 IEEE754 标准诞生了。
IEEE754
IEEE754 采用移码来表示阶码,规定了偏移量的选取;采用原码来表示尾数。从而统一了浮点数的表示。
整数的编码规则
原码
原码,原码,个人理解,就是很原始的码,是直觉上来对整数进行机内表示。
原码的结构也很简单。最高位作为符号位,1 表示负数,0 表示正数。而剩下的低位表示数的绝对值。
这种想法是很直接的,既然要表示正数和负数,那我就单独开辟一个符号位作为 flag,来标志数的正负。我们不妨来看几个数,以 8 位为例。

原码的问题是,在 0 的表示上有二义性;而且,如果要让有符号数和无符号数的加法使用同一个电路,很明显是不可行的,比如上图中的 $-0 + 1$,结果会被解释为 $-1$。
反码
因此,有人想出了反码来编码。正数的编码不变,负数的编码是其绝对值编码按位取反的结果。最高位可以理解为符号位,1 负 0 正。
不过因为反码只解决了用无符号数加法器的问题,但没能解决 0 的二义性,所以用的很少。看几个例子作为结束吧:

补码
要解决 0 的二义性,补码应运而生。
补码的规则是这样的:对于正数,补码 = 原码;对于负数,补码 = 负数绝对值的原码取反加一。
此外,注意到,最高位仍然可以看做是一个符号位,1 表示负数,0 表示正数(和 0)。
以 8 位为例:

补码和真值的互变是常用、常考的。正数的就不说了,平凡,对负数的来讲,总结下来,有这样三条路:
取反 + 1 流派
真值到补码:求负数的绝对值 -> 用原码/补码(一个意思)表示 -> 取反 -> + 1
补码到真值:补码取反 -> + 1 -> 加负号
更快的取反 + 1
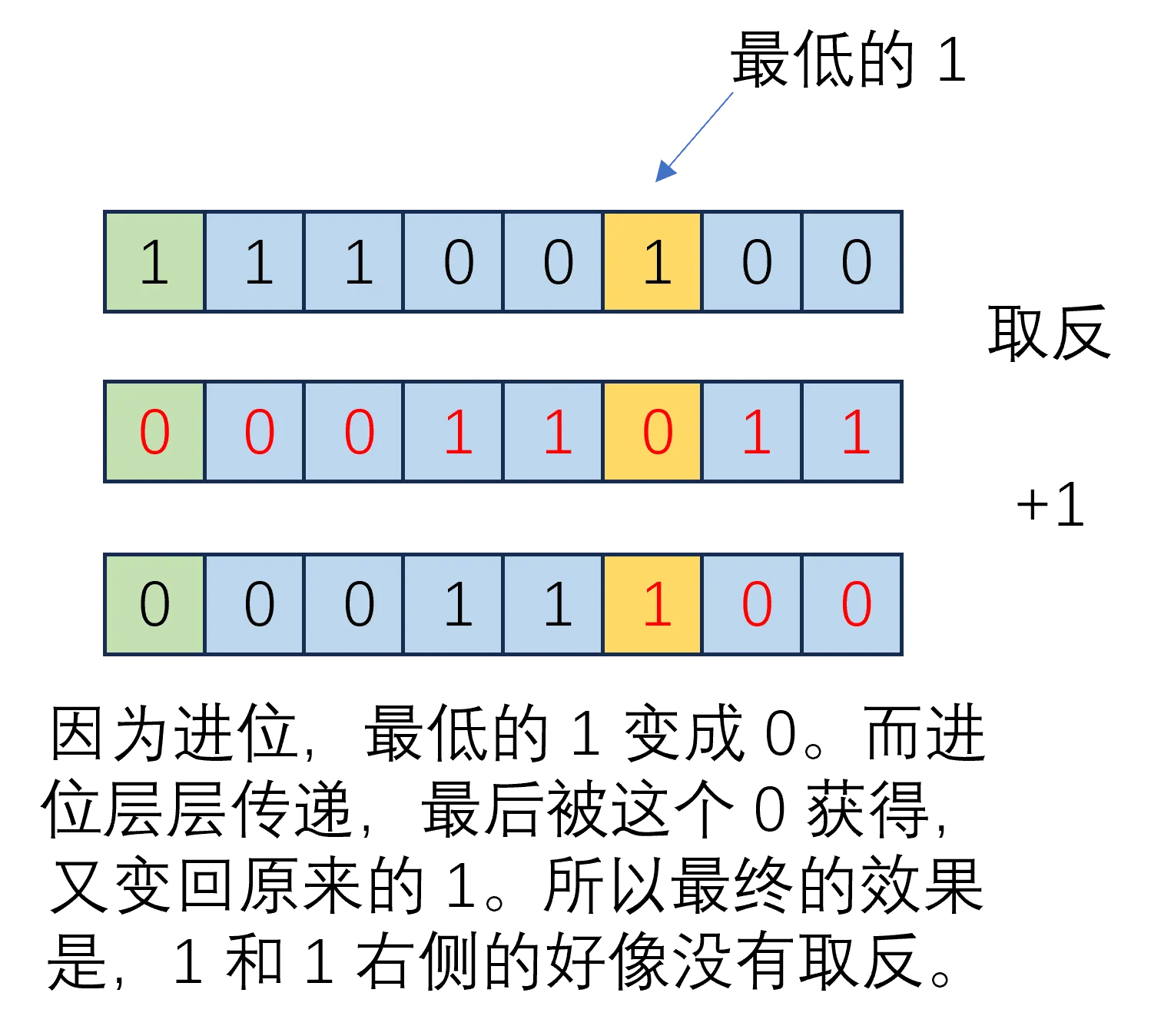
真值到补码:求负数的绝对值 -> 用原码/补码(一个意思)表示 -> 从最低位开始,找到第一个 1,1 左侧的取反(不含 1),1 和 1 右侧的保持不变
补码到真值:补码从最低位开始,找到第一个 1,1 左侧的取反(不含 1),1 和 1 右侧的保持不变 -> 加负号
这是可以在数学上证明的。
从最低位开始,找到第一个 1,这样,1 右侧的都是 0。取反 + 1,右侧的 0 变成 1,再加 1,又变回了 0,进位给到原来最低位的 1。但是因为 1 也被取反了,所以被取反后的 0 和进位 1 相加,$0 + 1 = 1$,也回到了 1。
此外,如果 1 就在最低位,右侧没有 0,也是适用的。
提供一张图,展示如何从补码得到真值:
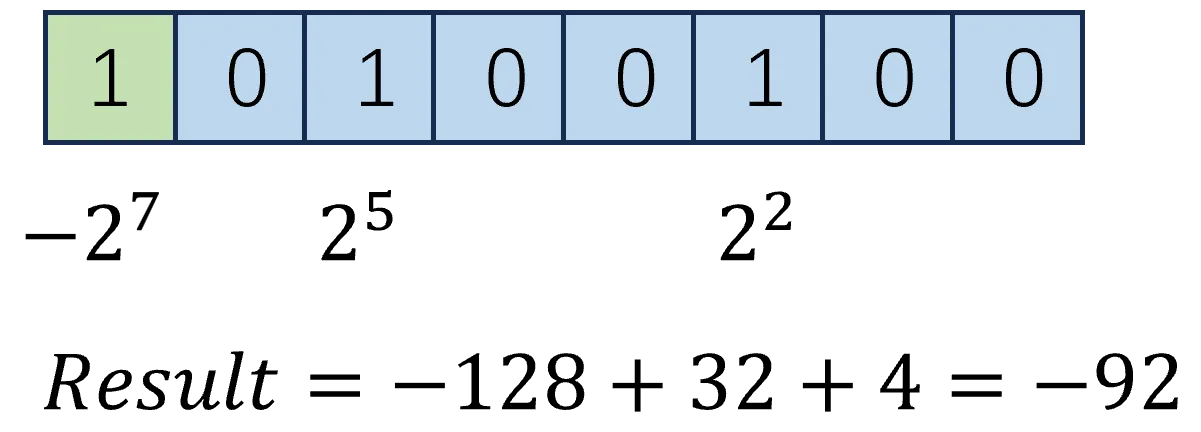
最高位的位权是负的
CSAPP 或者一些国外的教材喜欢这样解释,最高位的位权是负数,从而构成了真值。这对于一些位数比较小的二进制数来说,计算很方便,
读者可以用取反 + 1 的做法来看看,结果应该是一样的。
小数的编码规则
定点数中的纯小数
定点数中,纯小数是常考的。纯小数就是指绝对值 < 1 的小数。虽然数域扩大了,但是表示的原理和整数是一样的。
如果用原码来表示,最高位的值决定符号,低位数值位决定绝对值的大小。
如果用补码来表示,仍然沿用补码的规则。最高位的位权是 $2^0$,小数从小数点开始的位权依次降低,分别是 $2^{-1}, 2^{-2} \ldots$
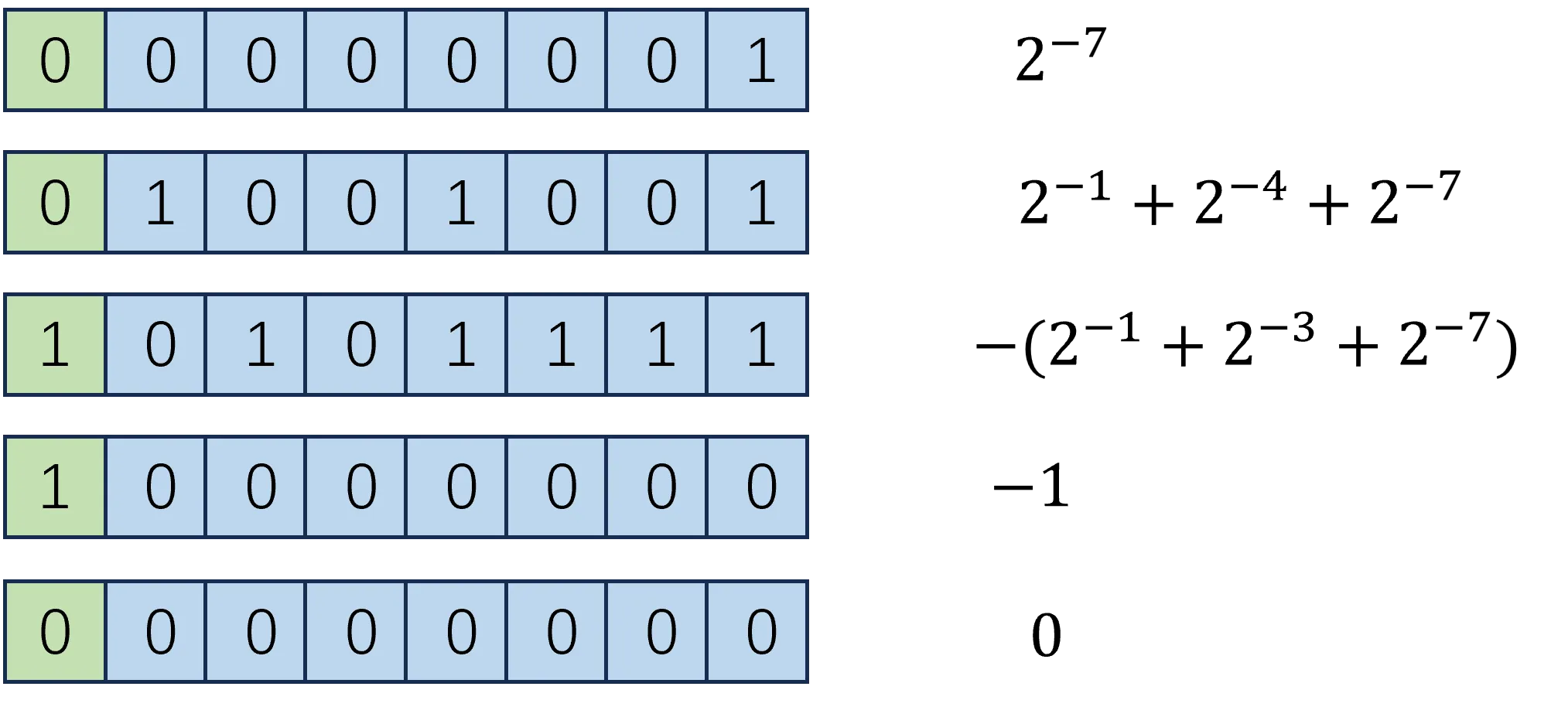
看几个例子,用原码来表示:

再看看同样的编码解释为补码纯小数的效果:
浮点数
浮点数沿袭了科学计数法的记法,只不过修改了一下指数和尾数的顺序。最终形成了下图的结构:

总的来说,符号位决定正负;阶码决定范围;尾数决定精度。
阶码的表示
阶码的表示用移码,移码的编码值是真值 + 偏移量。为了让表示的范围能尽量对称地表示正指数和负指数,所以要选择尽量中间的值作为偏移量。选哪个呢?
因为不论用多少位表示阶码,能表示的指数一定是偶数个($2^n, n: bits \geq 1$),总会偏上或偏下,没有正中间。所以,不妨选中间偏上的 10000...0 作为偏移量吧!
举个例子,如果用 8 位来表示阶码,那么,偏移量就是 128。如果一个小数是 $a.bcd \times 2^{-4}$ 的形式,那么 -4 在机内就会按照 124 来存储。$124_{10} = 7C_{16} = 0111\ 1100_{2}$
这里有一个技巧,那就是,偏移量为 $2^{n-1}$ 时,一个数的阶码和补码符号位是相反的,其余位不变。还是上面的例子,-4 的补码是 11111100,那么它的阶码就是 01111100,和我们用定义运算得到的结果是一样的。
这里还有一个结论,那就是对于阶码来说,1 表示正数,0 表示负数,和其他编码的符号位意义是相反的。
尾数的表示
尾数可以用原码或者补码的形式来表示。注意,这里要把符号位和尾数看做一个整体,作为数值位,然后,用前文定点数的结论来分析就好了。
但这里要注意一点不同,那就是,尾数的表示需要规格化。规格化的意义,我认为有两个:
- 消除二义性;
- 表示更高的精度。
第一点是显然的,如果不规定每个数唯一的表示形式,底层的电路又该如何解释分析?
第二点也好理解,如果把宝贵的尾数位存放一堆无用的、完全可以用阶码来表示的占位 0,不是一个好的选择。例如,$0.12345678$ 如果用 $0.0012345678 * 2^{-2}$ 来表示,如果尾数只有 8 位,那么第二种表示就会丢失精度。因此对规格化的规定是这样的:
- 如果是原码,要求是
0.1xxxx或者1.1xxxx的格式,换言之,十分位要是 1; - 如果是补码,要求是
0.1xxxx或者1.0xxxx的格式,换言之,最高的两位满足异或关系。
读者可以思考一下,上面的编码规则能不能满足规格化的两点要求?
以及,明明补码可以表示 $-\frac{1}{2}$,为什么不把它设计为合法的规格化格式呢?(提示:从电路设计的角度来思考,如果把它加入规格化格式中,还能用一个简单的异或逻辑来判断吗?)
在运算的过程中,有可能发生溢出(上溢 or 下溢)。因此把原先最高位符号位再复制一个,扩展为两位,然后再计算。如果溢出了,两个符号位不同,需要再次规格化。可能需要向左或向右移动小数点,具体看编码的规格化格式。
IEEE754
IEEE754 标准沿用了浮点数的表示结构,但在一些细节上有不同,从而解决浮点数的一些问题。
字长就那么大,精度的占比和范围的占比此消彼长,需要权衡。所以 IEEE754 对它们的占比是这样规定的(32 位机器):
float,单精度浮点型,32 位,1 位符号位,8 位指数位,23 位尾数位;double,双精度浮点型,64 位,1 位符号位,11 位指数位,52 位尾数位。
2008 版的标准还规定了一些其他字长的浮点型,从略。
更高的精度
IEEE754 对规格化的标准和上面的不同。首先,IEEE754 选择 原码 来编码尾数。而它要求规格化的位数格式为 01.xxxx 或 11.xxxx,即 s1.xxxx,其中 $s$ 表示符号位。
和科学计数法的思想类似。在科学计数法中,我们要求小数点左侧必须是一个一位的非零数。在二进制中,这个数不像十进制那么丰富,只能是 1。
这样的话,因为规格化要求符号位后方一定有一个 1,这样的话,就不用 1 位的空间存这个 1 了,而是把它作为隐含的 1。由此,IEEE754 就可以用 $n$ 位来实现 $n+1$ 位的精度。
更大的范围
不知道读者思考过没有,浮点数的表示是有 bug 的,那就是,怎么表示 0 呢?
思考几秒钟…
看看原码的定义,十分位必须是 1,那就是绝对值最小也得是 $\frac{1}{2}$。天大的笑话!前面的编码都在想解决 0 的二义性问题,结果到了浮点数,居然无法表示 0 了?
幸运的是,IEEE754 标准通过把某几个阶码设置为标志位,从而达到了这一目的。
首先,IEEE754 对于偏移量的选择,并不是$2^{n-1}$,而是中间偏下的一位:$2^{n-1}-1$。我想出来一个 「双减」作为口诀。
这样的话,阶码和补码之间符号位反转的结论就不成立了。真值的范围,是正数比负数可以多表示一位,如果还是以 8 位为例,那就是 -127 ~ +128,对应二进制为 00000000 ~ 11111111。
但是!
二进制全 0 和全 1 作为标志位,不表示某一个具体的阶码值。所以阶码的表示范围是 -126 ~ +127
如果为全 0,说明这个阶码非常小,很接近 0 了。
所以,如果在阶码为全 0 的情况下,尾数为全 0,则表示 0。
而如果尾数不全为 0,则可以用来表示非规格化的小数。这里的非规格化,指的是符号位右边那个隐含的 1 不要了,当做 0 来处理。这样就可以表示那些更接近 0 的值。此时的阶码是在阶码的表示范围内最小的那个,如果是 8 位的,那就是 -126。
如果为全 1,说明这个阶码非常大,很接近无穷了。所以,如果此时尾数为全 0,则表示无穷大,根据符号位的不同可以表示 $-\infty$ 和 $+\infty$。
但如果尾数不为全 0,则说明计算出了问题,得到的结果是「非数」,NaN,aka Not a Number。比如给一个负数开平方根就会得到 NaN。
一个真值和编码值转换的例子
应试角度上,看个例子吧:
如何把 $22.78125$ 转换为 32 位的 IEEE754 浮点数?
先确定符号位,正数,所以是 0。
再确定尾数和阶码,需要把小数转换成二进制表示。整数部分的转换很简单,16H,小数怎么办呢?
有两种方法。课内常教的是乘二取整,从下往上抄结果,因为越乘阶越高,那就越靠近小数点。
还有一种方法是 CSAPP 上提到的,那就是转换成分数。
比如说:
$$
0.78125 = \frac{78125}{100000} = \frac{25}{32} = \frac{25}{2^5}
$$
$\frac{25}{2^5}$ 的意思是,把 25 按位右移 5 位。也就是说:
$$
(25){10} \div 2^5 = (11001){2} \times 2^{-5} = (0.11001)_{2}
$$
所以也不用费劲除啦,约分得到的分母的二进制表示就是小数部分。
所以我们得到了 10110.11001,规格化一下,是 01.011011001 * 2^4。
所以阶码是 4 + 127 = 131 = 83H = 10000011,尾数是 0110110010000...0。
最终拼起来:0100 0001 1011 0110 0100 0000 0000 0000,也就是 0x41B64000。
浮点数的表示范围
这里以 float 为例,以正数为例,因为尾数是原码表示,是对称的。
有四个数我们比较在意:规格化最大,规格化最小,非规格化最大,非规格化最小(不考虑 0)。
规格化最大:
阶码是 1111 1110,也就是 +127。尾数是 11111....1,也就是 1 - 2^(-23)。最后得到 $(2 - 2^{-23}) \times 2^{127} = 3.402823466 \times 10^{38}$。
想想为什么是 $2 - 2^{-23}$,而不是 $1 - 2^{-23}$ 呢?
规格化最小:
阶码是 0000 0001,也就是 -126。尾数是 00000....0,也就是 0。最后得到 $1 \times 2^{-126} = 1.175494351 \times 10^{-38}$。
想想为什么是尾数可以取到
00000....0,而不是00000....1呢?
非规格化最大:
阶码是 0000 0000,特殊标记,也就是 -126。尾数是 11111....1,也就是 1 - 2^(-23)。最后得到 $1 - 2^{-23} \times 2^{-126} = 1.175494211 \times 10^{-38}$。
想想为什么是 $1 - 2^{-23}$,而不是 $2 - 2^{-23}$ 呢?
非规格化最小:
阶码是 0000 0000,特殊标记,也就是 -126。尾数是 00000....1,也就是 2^(-23)。最后得到 $2^{-23} \times 2^{-126} = 1.401298464 \times 10^{-45}$。
想想为什么是这次尾数不是
00000....0了呢?
还有一个 FLT_EPSILON,float.h 的注释是这样说的:// smallest such that 1.0+FLT_EPSILON != 1.0。那不就是精度的意思嘛!
此时的阶码应该是 0,而 $\varepsilon = 2^{-23} = 1.192092896 \times 10^{-7}$。
浮点数的精度
我们说,float 有 7 位精度,这是怎么来的呢?
因为在机内,尾数通过 23 位达到了 24 位的精度,也就是能表示 $2^{24}$ 个数,不过人是使用十进制的,所以能表示多少位呢?需要进行这样的换算:
$$
10^{?} = 2^{24}
$$
一个对数运算可以求得 $? = \log2^{24} \approx 7.22$,位数是要下取整的,所以是 7 位。
我们说,double 有 15 位精度,为什么呢?因为在机内,尾数通过 52 位达到了 53 位的精度,也就是能表示 $2^{53}$ 个数,同样的对数运算可以求得 $ log2^{53} \approx 15.95$。
拓展:非规格化数可以解决的问题
如果 IEEE754 标准中没有非规格化数,又会怎样呢?
假设三位阶码,可以表示 -2 ~ 3(因为 -3 和 4 是标志位)。试想这样两个数:
$$
x = 1.011 \times 2^{-1}
$$
$$
y = 1.001 \times 2^{-1}
$$
$$
x - y = 0.0010 \times 2^{-1} = 1.000 \times 2^{-3} = 0
$$
注意到明明 $x \neq y$,但二者相减后却为 0。这对于一些除法程序很不友好:
1 | |
不过如果有渐进下溢的存在,可以用非规格化数表示 $x - y$ 的结果:
$$
x - y = 0.0010 \times 2^{-1} = 0.100 \times 2^{-2} \neq 0
$$
问题解决。
