计组 | 浮点数的运算

说在前面

浮点数的运算步骤比较多，而且种类也比较多。

运算数的不同会影响运算进行多少步；而运算数的表示方式（原码、补码、移码）会影响具体问题的分析。

浮点数的加减法

加减法大概需要这样几步：

1. 对阶。小阶向大阶对齐，否则大阶的高位被舍去，误差太大；
2. 尾数的相加；
3. 规格化；
   • 左规
   • 右规
4. 舍入处理；
   • 截断；
   • 末尾恒置 1；
   • 0 舍 1 入。

看看流程图吧：

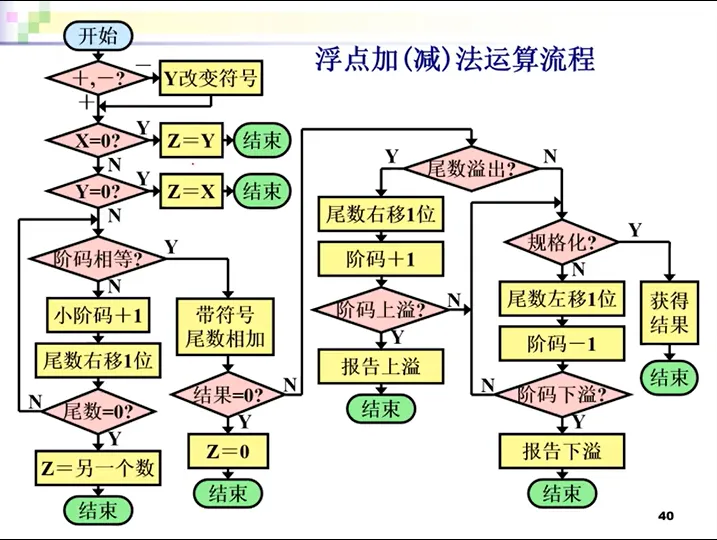
所以如果理解了这一个过程，就会明白，为什么浮点数中，一个很大的数加很小的数会损失精度了。

浮点数的乘除法

浮点数的乘除法，要经历如下的阶段。不用文字了，直接展示流程图：

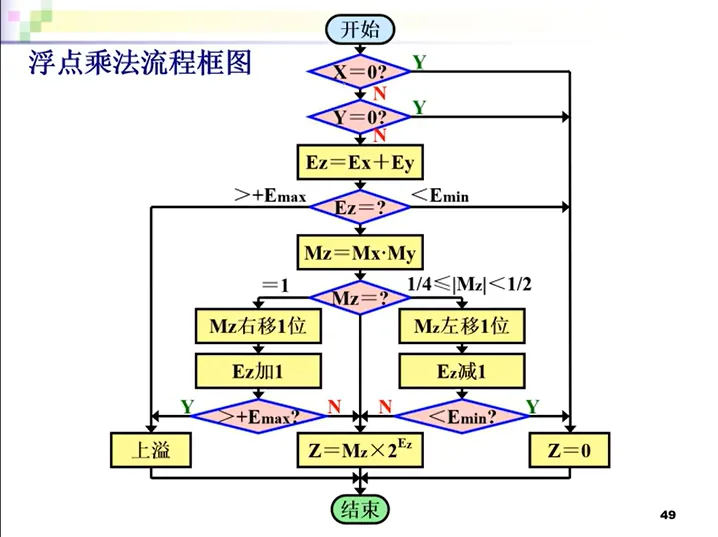
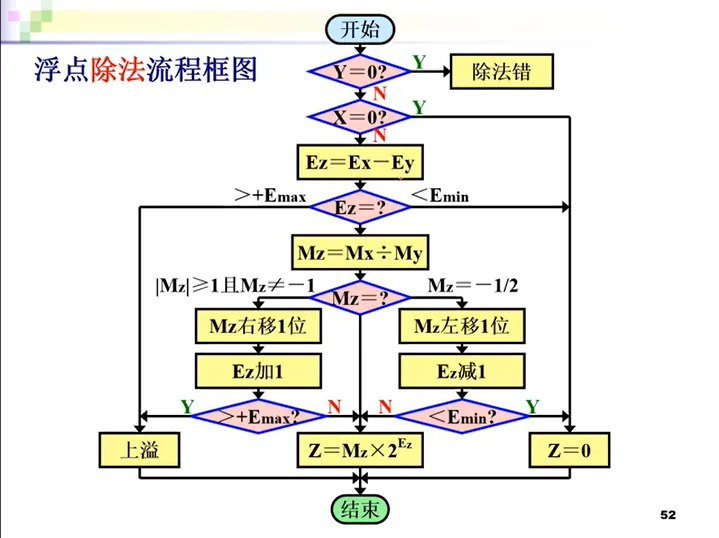
这里常考的一类题目是到底需要规格化几次，需要明白原码或补码表示时，数值的范围。

有时候是 0 次，不过最多是一次。

说明的是，在加减法和乘除法的过程中，如果使用更大的扩展位，可以提高精度。例如，Intel 在实现浮点数运算的时候，采用 80 位扩展，等保存结果的时候，再截断到 float 或者 double 的长度。