计组 | 数据的运算

加法

之前说过，补码的好处就在于可以直接使用无符号数的加法器硬件。因此，这里说的加法都是补码的加法，当然还涉及到了浮点数的阶码加法运算。

理论

在进入到硬件层面之前，需要对加法进行理论分析，尤其是溢出判断的部分。判断溢出有如下几种方法：

1. 双符号位；
2. 进位；
3. 符号位和进位标志；
4. 运算前后的符号位（正 + 正 == 正？负 + 负 == 负？）。

3、4 只适用于同号数求和 or 异号数求差的判断，用得少。

1 在加法运算中对两个 operand 用两个符号位，如果运算结束后两个符号位不一样，那说明发生了溢出，表明当前的长度表示不下结果。扩展后的高位符号位肯定是真的，但是在结果中会被截断，低位的符号位会被保留。所以如果低位的符号位和最高位的符号位不一样，说明最终的符号位不符合预期，发生溢出。

2 记录最高位和次高位的进位情况，二者的异或表示是否发生了溢出。用穷举法证明，思路是：证明异号运算不会满足溢出判断的标准；再证明同号运算用此标准可以判断是否溢出（思路是：如果结果的符号位和加数一样，考察两个进位；如果不一样，也就是溢出了，再考察两个进位情况）。

行波进位加法器

到底是念 xing 还是 hang 呢？见仁见智。

行波进位加法器的基本单元是一位全加器，数字逻辑中已经对它很熟悉了。把多个全加器级联起来就可以完成多位运算。

优势：便于扩展，逻辑简单；

不足：延迟高。

超前进位加法器

通过对加法运算的分析，可以得到输出结果和每个原始输入的关系，这样就不必向前面的加法器一样要逐级向上传递进位信号了。

优势：速度快；

不足：门的数量多。

所以一般实践上把二者结合起来，比如，超前进位加法器组成四位加法器，每个四位加法器之间串联行波进位。

BCD 加法

有时候需要对 BCD 编码的数进行加法运算。牢记：当运算结果中某位数大于 9 或者有向更高位的进位，则结果的对应位 +6 修正。

前者好理解，如果某位数大于 9，压根不是合法的 BCD 编码，1234 是合法的 BCD 编码，但 12A4 不是。为什么不是呢？因为这个 A 应该有一个进给更高位的进位。究其原因，就是因为实际上，底层用的是 16 进制来表示 10 进制的运算。

后者为什么呢？比如，有个位的结果算出来是 18，向更高位进位了一个 16，这位剩下个 2。这对吗？这不对，为什么？进位多了，按十进制，应该进个 10 啊，怎么进了个 16 呢？所以还是要修正一下。

所以最后再分类概括一下：

• 如果结果位在 $[0, 9]$，正常表示，没什么说的；
• 如果结果位在 $[10, 15]$，在十进制中应该进位了，但是在 16 进制中却仍然能表示，所以欠了个进位；
• 如果结果位在 $[16, 19]$ 的，是该进位，但是应该进 10，而不是 16，要把进多了的 6 补回来。

移码加法

这里指的是标准移码，偏移量最高位为 1，剩余为 0。

通过数学的推导，可以得到，

$$
[X+Y]{移} = [X]{移} + [Y]_{移} - 2^{n-1}
$$

也就是说，直接移码相加，然后符号位取反即可。如果符号位不取反，其实就是补码。

此外，若已知一个数的移码表示，其相反数的移码表示是取反 + 1（也就是求补运算）。

乘法

原码一位乘

因为是原码，所以符号位单独处理，只考虑绝对值之间的运算。

从乘法的竖式中也可以悟到，其实乘法就是移位和相加操作的反复。因此在硬件层面上也是这样实现的，只不过在竖式乘法中，每次得到的结果左移，在硬件实现上，结果要右移。

用伪算法来表示一下硬件实现的流程吧：

while (没考虑完乘数的位数) {
    if (最低位为 1) {
        加乘数;
    }

    右移一位; // 这句没有缩进到 if 语句块里！
}

看看具体在答题时如何做呢？

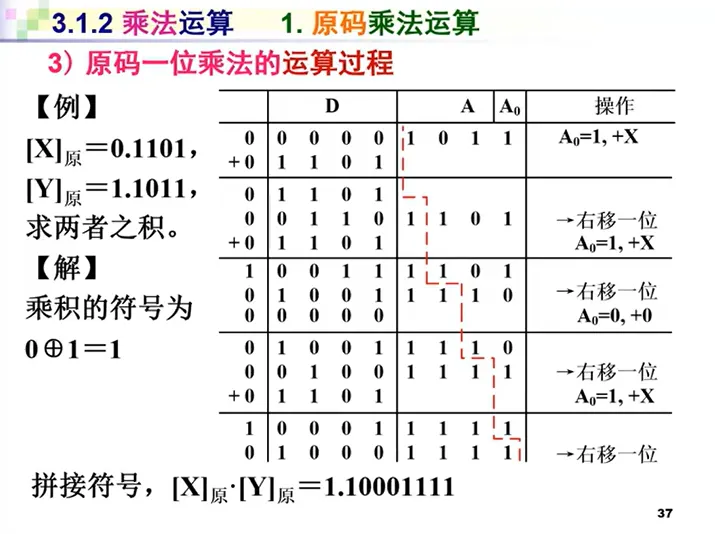
这里给一些注释：

• 表头中，最左侧不是符号位（已经是绝对值的运算了），而是存储可能的进位；
• 表头中，$D$ 用来存储结果的高位，初值为 $0$；$A$ 一开始存储了一个乘数，最后存储了结果的低位；$A_0$ 用来显式标注是否需要加乘数；
• 个人认为，操作块的划分看自己心情，只要有逻辑就好。

最后记得把符号位拼接起来。

补码一位乘

在进行补码乘法之前，先推导出来了一个结论，即从补码得到真值，可以通过简单的位权的运算来得到真值，只不过注意最高位要加个符号即可。

比如，四位整数表示 1011，可以通过：

$$
-2^{3} + 2^{1} + 2^{0} = -5
$$

注意负号的位置。

常用的方法是布斯 (Booth) 法。只需要对乘数进行一个微小的修正（判断是否加乘数的依据从最低位变成了最低位减次低位），就能沿用原码乘法的规则。

还是用伪算法来表示一下运算步骤：

while (没考虑完乘数的位数) {
    switch ({次低位,最低位}) {
        case {0, 0}
        case {1, 1} {
            break;
        }
        case {0, 1} {
            + [X] 的补码;
            break;
        }
        case {1, 0} {
            + [-X] 的补码;
            break;
        }
    }

    右移一位;  // 感觉最后一步移位不移位都行
}

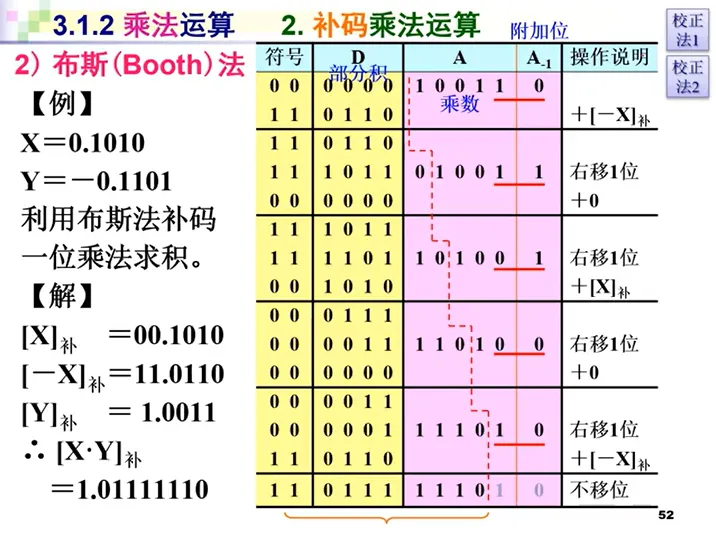
• 表头左侧最高位是两个符号位，两个是为了防止溢出；设置符号位是因为正在进行补码运算；
• $A$ 中存放的是带符号位的乘数的补码；
• 需要附加一个 $A_{-1}$ 来形成循环；
• 右移是算数右移。

矫正法

根据乘数的正负，如果决定循环次数的是负数的话，需要最后一步进行修正。

用得少。

阵列乘法器

上面的方法有个不足，和行波进位加法器一样，那就是太慢了。

通过手算的原理，可以发明阵列乘法器。

无符号数的比较简单。如果有符号数，需要增加一个求补电路转换为无符号数，最后再通过求补电路得到结果。

流水线阵列乘法器

（原码）除法

除法只要求原码的。能进行除法有两个基本要求：

1. 除数不为 0；
2. 被除数的高 $n$ 位的值要小于除数的位数 $n$。

第一点是显然的，第二点主要是为了保证商不会溢出。如果 2 不成立，商可能就有 $n+1$ 位，表示不下了。

恢复余数法

废话不多说，直接上伪算法：

while (商的位数小于被除数位数的一半) {
    左移 1 位;  // 因为第一步肯定不够减
    减去除数的绝对值;
    if (结果的符号位为 0 ) {  // 够减
        最低位置 1;
    }
    else {  // 不够减
        最低位置 0;
        加上除数的绝对值;
    }
}

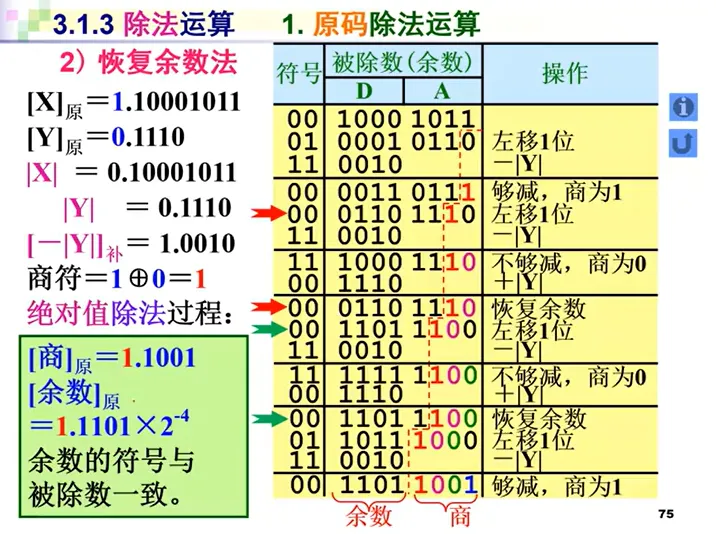
• 防止符号位溢出，置两个符号位，因为左移的时候数值位会侵占一位符号位；
• 运算需要左移，就像乘法右移一样；
• 每次判断是否够减，根据符号位判断；
• 如果不够减，要把多减的数值加回去；
• 减法是通过补码实现的。

余数记得 $\times 2^{-m}$，商和余数符号位单独处理。

加减交替法

注意到：如果某一步多减了 $A$，把多减的加回去，位移后再减 $A$ 等价于 多减了 $A$，位移，再加回去 $A$。

这样就省去了加回去的步骤。

来看伪算法：

左移 1 位;
减去除数;

while (商的位数小于被除数位数的一半) {
    if (余数 >= 0) {
        商上 1;
        余数左移 1 位;
        减除数;
    }
    else {
        商上 0;
        余数左移 1 位;
        加除数;
    }
}

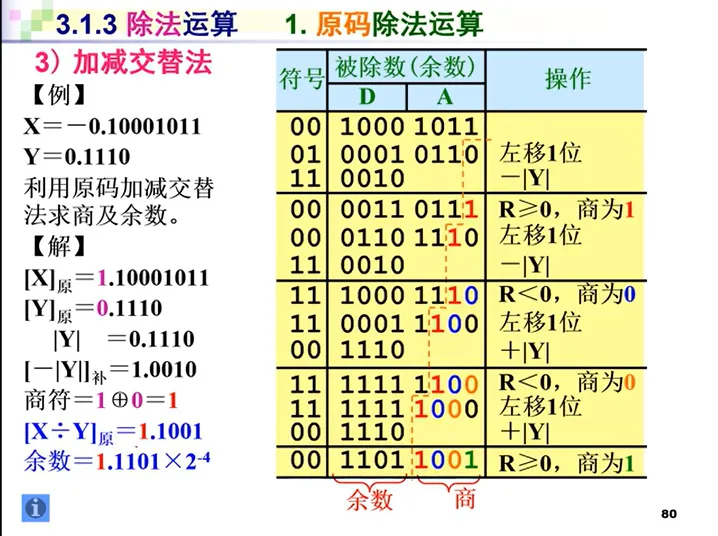
基本要说明的和上一个方法一样。主要是改进了不够减要加回去的问题。

阵列除法器

当然，追求速度，有阵列除法器的存在，它的设计原理是基于加减交替法的。

（补码）除法

补充一下，发现学校要考补码除法中的加减交替法，所以展示一下流程。

加减交替法

while (商的位数小于被除数位数的一半) {
    if (除数和余数异号) {
        余数加除数;
        商上 0;
    }
    else {
        余数减除数;
        商上 1;
    }

    左移一位;
}

• 采用双符号位，同上；
• 末尾商恒置 1，误差可以接受；
• 商需要多考虑一位；
• 注意如何表示最终的商和余数。

其实，补码的加减交替法和原码的大差不差，区别在：

• 数的表示不同，需要考虑双符号位；
• 符号位参与运算，所以商要多一位；
• 加减的判断条件略有变化。

因为作图不太容易，就不作了。一个和先前 ppt 风格不一样的图片可以参考博客园-【计算机组成原理】 补码的除法运算– 加减交替法。

但其实也可以用之前的形式来表示。