0. 序

搜索是人工智能领域很重要的内容，例如如何导航到目标地点，如何在游戏中获得胜利等等，都需要进行最优方法的选择。哈佛大学的 CS50 AI 课程把它作为了课程的第一课。听完后醍醐灌顶，赶紧趁热写一篇文章，把大意整理下来，供未来自己复习。

1. 单机游戏

1.1 一般的搜索

给定一张有向图，从某个节点寻找前往另一个节点的道路，这很简单。关键在于维护一个 Frontier 列表，然后重复进行如下的操作：

1
2
3
4
5
6
1. 如果 `Frontier` 列表为空
    * 则中止，无解。
2. 从中选取一个结点，作为要考虑的结点。
3. 如果这个结点就是目标
    * 则返回解，停止。
4. 否则，考察这个结点的邻居，把邻居添加到 `Frontier` 中

当然这样的选取有一些问题，不妨考虑这样的一个有向图，其中 A、B 两个结点之间有双向的箭头。把 A 作为起点。

这样的问题是，Frontier 中一开始只有 A，A 不是终点，所以考虑和 A 连接的节点，假设只有 B，所以把 B 放到 Frontier 中。现在从 Frontier 中取 B，B 也不是终点，考虑 B 能连接的节点，假如有 A 和 C。那么 A 和 C 加入到 Frontier 中，下一次再考虑 A。如此反复，就进入了一个死循环。

因此，在第 4 步需要增加一个判断：只有没有访问过、并且不在 Frontier 中已经出现的节点，才会添加到 Frontier 中。这样就避免了回环的问题。这，就是最基础的搜索。

我学到这里最深切的感受是，总算明白为什么 Dijkstra、Kruskal 等算法一开始的时候要把初始数组设置为只包含起点了，因为这个维护的数组表示的是可以访问到的节点，而一开始，只有起点可以访问到。

前面的搜索的伪算法，并不能算是一个很好的算法，因为它在一个语句上表述得并不具有确定性，也就是 选取 二字。怎么选？这就引出了两种不同的搜索算法：深度优先搜索和广度优先搜索。

下面的算法都以迷宫作为背景。

1.2. DFS

深度优先搜索对于 Frontier 的维护采用栈来作为数据结构，Last In, First Out。直观造成的效果就是一条道走到黑，只有走到死胡同才会回头。而且这回头不简单——好像回到了存档点一样，从最近的分岔路口再次开始，选择另一条道路，再一次地走到黑。这就体现出栈这一数据结构具有保存现场的作用啦！

深度优先搜索的好处是，在起止点相距较远的情景下，占用更小的内存，就能找到可行解。但不足是，它并不能确保每次找到的解是距离最短的最优解。

1.3. BFS

广度优先搜索和深度优先搜索唯一的区别就在于 Frontier 的维护，BFS 采用队列作为数据结构，First In, First Out。达成的效果是一种层次遍历，就像古诗说的：

泻水置平地，各自东西南北流。

BFS 就像在起点洒了一桶水，水在到达终点之前，会蔓延到所有与起点距离小于等于起止点距离的格子。但这样有个好处，就是可以确保找到的是最优解。证明也很简单，不妨用反证法。假如存在一条路径，使得起止点之间的距离更短，那么根据 BFS 的原理，这条路径应该早就被蔓延到了。

不过 BFS 当然也有缺点，那就是需要的内存比较多，它需要多线程般探寻多条路径，才能得到最终的结果。如果起止点的距离相距太远，甚至会搜索完整个迷宫空间。

1.4. 贪心”最佳优先”搜索

之前讲的 BFS 和 DFS 都是无信息检索，也及时没有用到具体问题的背景知识，所以显得没那么智慧。怎样就能更智慧了呢？比如让人类来走迷宫，给他一张纸，左下角是起点，右上角是终点。人直觉地在面对岔路口时，就会选择向右的、向上的，因为在不考虑墙的前提下，确实离终点越来越近了。这就是一种贪心算法。

在岔路口面临抉择的时候，到底怎么选？BFS 和 DFS 并没有给出选择的不同，所以这样随机的选择往往会走不少低智商的弯路。有人说啊，那不是一个从前面 pop，一个从后面 pop 吗？但这只是指定了退出的顺序，没有指定进入的顺序呀。比如列表里有 ABC，你说，用栈的话就是 CBA，用队列就是 ABC，确实是这样。但并没有保证每次进入的时候都是 ABC 啊，进入的顺序还是随机的，可能下次就是 BCA，CAB 了。这样的话，最终选择还是随机的。

而贪心算法则不一样，对每种选择，通过启发函数得到一个值，在迷宫的问题背景下就是下一个格子和终点之间的曼哈顿距离（曼哈顿距离就是只能横平竖直地走，不能走对角线），最后选取距离小的。这样就能和前面的两种搜索找出不同了——不管程序运行多少次，选择的路径肯定是一样的，没有半点随机因素，小就是小，大就是大。

1.5. A* 搜索

但是贪心算法也不一定是最优解，因为它眼光是狭窄的，未能远谋。在一个分岔路口，一边是 19，一边是 18，它就选择了 18。它哪里知道，19 是山坡的最高峰，再往后一马平川；又哪里知道 18 后面还要面临重峦叠嶂、蜿蜒曲折的山路呢？所以最终要表达的就是，如果在树林中有两条路，在当时的条件下选了 18，最后走的路可能比 19 多得多。

这样岂不是太傻了？除了曼哈顿距离之外，还有什么指标可以修正呢？啊，距离，距离！我通过 18 这个路口，走了 200 步才到了曼哈顿距离是 5 的格子；我通过 19 这个路口，再走14 步就到了距离为 5 的格子。这样看来，不仅要考虑启发函数的值，还要考虑得到这个值的代价！就好像参加 ICPC 拿到金奖就能在保研上获得很大优势一样，如果花了很大力气才能得金奖，不如中途停下来思考一下，当前距离目标的远近和自己已经付出的代价，如果发现不值当，不如马上切换到另一条路线。所以在 A* 搜索中，代价（这里是走的步数）+ 启发函数值的和才作为选择的判据。

这个方法很巧妙，比如就走迷宫这个例子，如果距离目标越来越近，代价 + 启发函数值是不变的，步数多了一个，后者少了一个，总和不变。然而若是稍微走了一点回头路，总和会 +2、+2、+2 进行下去，很快就会超过岔路口的另一个选择（如果二者差别并不悬殊的话）。

2. 对弈

2.1 Minimax

前面的搜索算法都是一个人的奋斗，但是在生活中，你方唱罢我登场的场面比比皆是，不仅要考虑自己的水平，还要衡量对方的能力，更有甚者，还得零和博弈。

这里以双方的竞争为例，让自己获胜，等价于让别人失败。对方呢，也是这样想的。人类知道获胜、失败的具体含义，但机器可不知道，怎样量化胜负这件事儿呢？不妨用数字啦！

对弈的双方，一方想让数字升高，另一方想让数字降低，如同拔河一般的拉锯战。Minimax 就是这样一种算法，一方要 minimize outcome，而另一方要 maximize it。至于说怎样得到所谓的最大值和最小值，其实是一种递归的思路。不妨以想要让结果变大的一方为例。

  1. 现在摆在它面前的是一场残局，轮到他走下一步。到底落子何处？有许多选择，这些选择分叉出来。

  2. 不管他选择哪种，现在的主动权到了对方手中。

  3. 对方想让数值尽可能的小，所以也要面对同样的思考方式。到底落子何处呢？又有许多选择，但不管哪种，现在又轮到结果变大的一方来落子了。

  4. 就这样循环往复，递归下去，直到最后分出胜负。这里我们只考虑相邻的两层，按照递归的经典分析方法。现在我们回到第 2 步，主动权到了变小的一方。假设这里可以得出棋局的最终值，分别是，6，5，4，7，2。那么，变大的一方就知道了，哦，我现在面临五种选择，分别让结果变大的个数是这些，我肯定选择更大的，所以选择了 7。因为这种选择是建立在对方下的是最优解的基础上的，所以，如果他选择了 4 甚至是 2，对方就会顺着这条路走下去，达到让结果变小的目的，这样是不好的。

不过这样有个问题，对于井字棋游戏这种规模小的游戏还好说，对于国际象棋、围棋那种对弈，层层递归下去，要大量的内存，花费时间多不说，还很有可能爆栈，能不能稍微减少点运算量呢？

2.2 α-β 剪枝

看这张图：

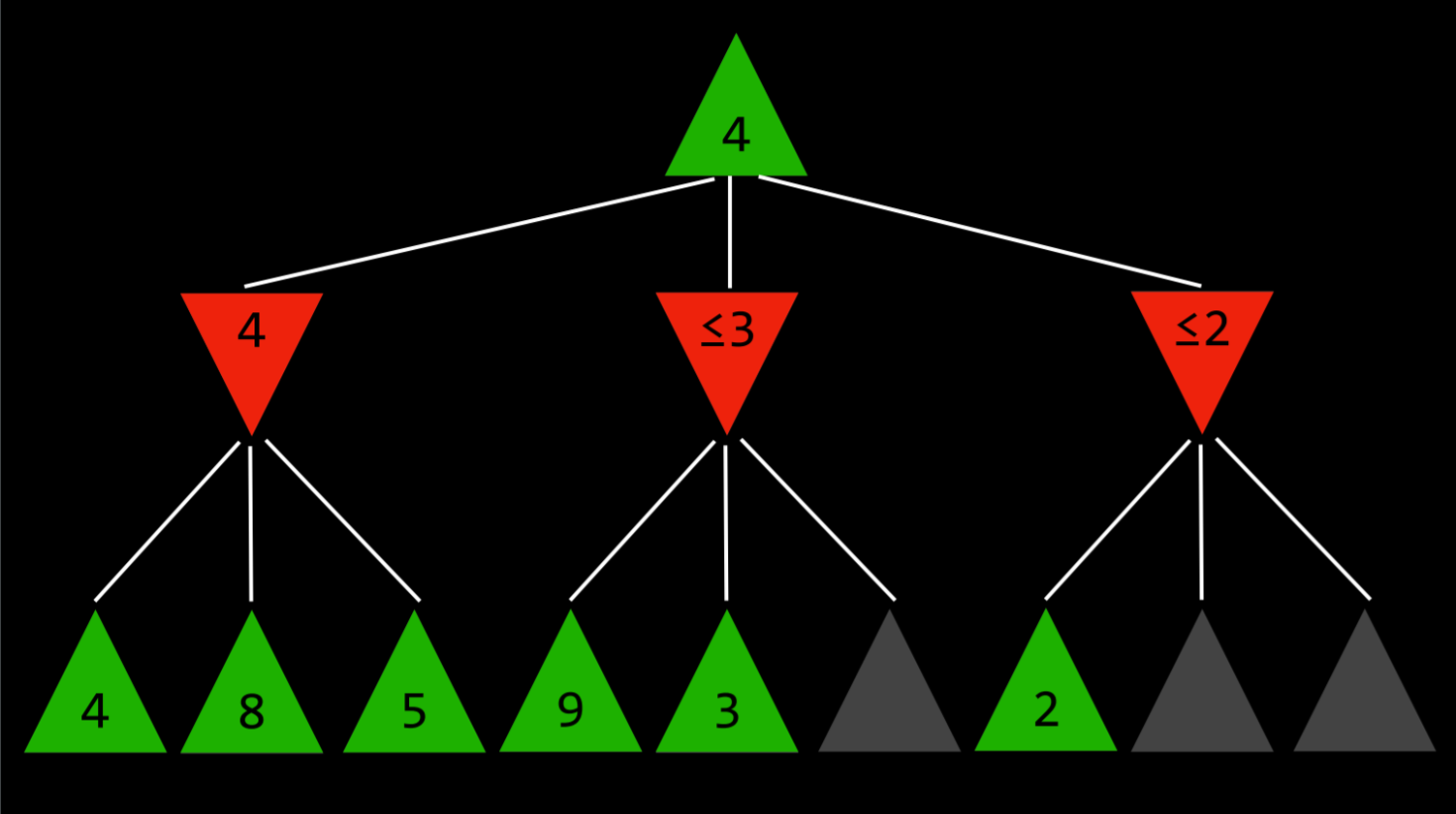
a-b(ref:https://cs50.harvard.edu/ai/2024/notes/0/)

现在最顶层的绿色想尽可能增大结果，不过在分析它的值之前，按递归的思路，先得看看底层的数值。第一个分支，选择最小的 4。第二个分支，走到第二步就知道，红色肯定 <= 3 了，也就是红色削弱数值增加的能力最弱也是 3，和第一个分支中，最强的削弱能力是 4 相比，不用考虑了。后面的 2 也是同理，看到第一个，就不用往后看了。这样的话，就可以减少大量的递归运算，层次越高，越有效。换句话说，就是预测到了这个分支顶天也就这种能力了，不如已经备选的分支，所以可以及时止损。

2.3 深度限制的 Minimax

你可能觉得，现在这种优化还是不够过瘾，因为毕竟在更复杂的游戏中，很难递归到终局的局面。所以有的时候，对递归的层数有限制，到了最深层后，通过另一个函数对残局进行评价，比如谁剩子多等指标来评判出谁占优势，从而生成一个值。这个相对没那么精确的值，就是上一层筛选的指标了。

3. 结语

以上就是有关搜索的全部内容，听起来很爽，也让我想到了人生中的一些抉择。当时学离散的第一课，老师就说，不知道同学们是不是已经接触过贪心算法了，贪心算法，有的时候不一定就是最好的。

是呀，竞赛？科研？甚至我有个朋友为了保研名额，在大一下的那个岔路口选择了去保研率更高的专业班型，他的选择是离终点更近的吗？我选择留在现在的专业，就保研来说，是最优解吗？

到底该用什么算法来走这一遭呢？